Branchless Programming
Mon 21 October 20241. CPU 파이프라인

-
CPU 파이프라이닝의 기초
-
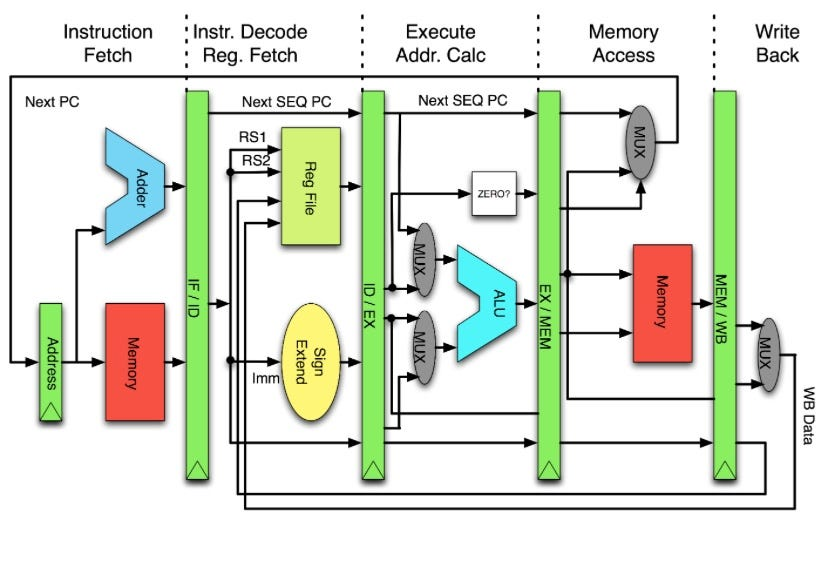
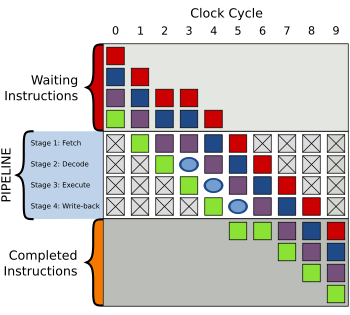
CPU가 명령어를 단계별로 처리하여 처리량을 향상시키는 방법 설명.
-
-
파이프라인 단계
- Fetch(인출), Decode(해독), Execute(실행), Memory Access(메모리 접근), Write Back(쓰기 반환).
- 파이프라이닝의 이점
- 명령어 처리량 및 CPU 효율성 증가.
-
파이프라인 해저드(Hazard)
-
구조적 해저드: 자원 충돌.
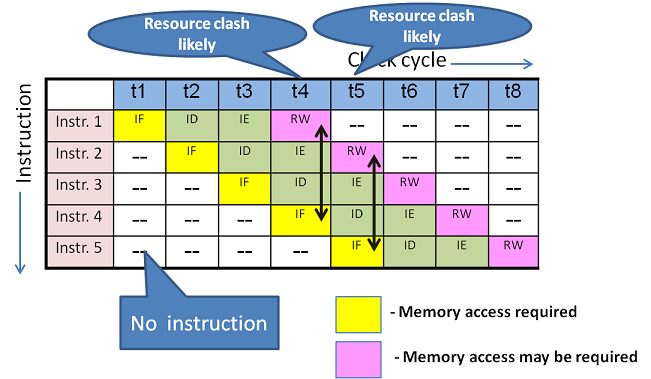
-
데이터 해저드: 명령어 간의 의존성.
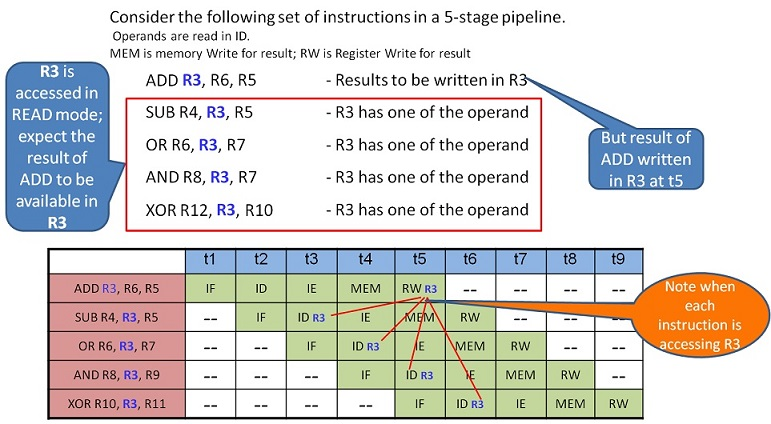
-
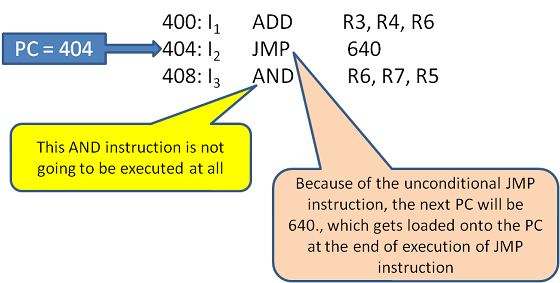
제어 해저드: 분기 명령어로 인한 파이프라인 플러시(flush).
-
2. 분기 예측
- 분기 예측이란?
- CPU가 조건부 연산의 결과를 추측하는 메커니즘.
- 분기 예측기의 종류
- 정적 예측: 고정된 전략(예: 항상 taken으로 예측).
- 동적 예측: 런타임 행동에 따라 예측을 조정.
-
분기 예측 알고리즘
-
1비트 및 2비트 예측기.
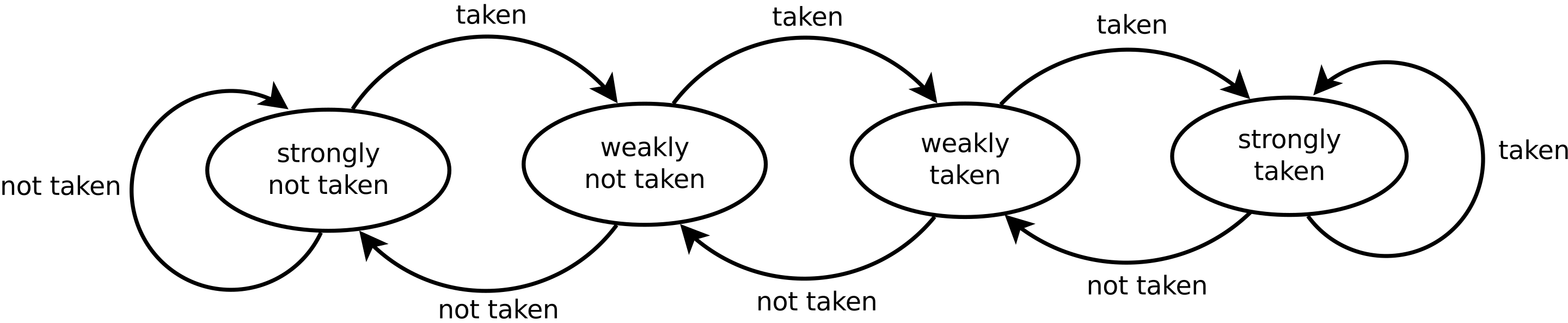
2-bit saturating counter
-
글로벌 및 로컬 히스토리 예측기.
- 정확도와 성능 영향
- 높은 정확도는 파이프라인 지연을 감소시킴.
- 오예측은 성능 패널티를 초래.
-
3. 분기 실패 패널티
- 분기 실패의 정의
- CPU의 분기 예측이 틀렸을 때.
- 파이프라인 플러시
- 예측 실행된 명령어를 버리는 과정.
- 성능 패널티
- 오예측으로 인한 사이클 손실.
- 예: 현대 CPU는 오예측당 15-20 사이클을 잃을 수 있음.
- 영향의 정량화
- 빈번한 오예측이 전체 애플리케이션 성능에 미치는 영향.
4. 분기 없는 프로그래밍
- 개념 개요
- 조건부 분기를 최소화하거나 제거하는 코드 작성.
- 분기 없는 프로그래밍의 이점
- 분기 오예측 감소.
- 명령어 수준 병렬성 향상.
- CPU 파이프라인 효율성 증대.
- 사용 사례
- 성능이 중요한 코드 섹션.
- 예측 가능한 제어 흐름을 가진 알고리즘.
5. 분기 없는 프로그래밍의 방법들
- 산술 및 논리 연산
- 조건부 로직을 대체하기 위해 수학적 연산 사용.
- 예: 비트 연산을 사용한 조건 검사.
- 조건부 이동 명령어
- 분기 없이 조건 플래그에 따라 데이터를 이동시키는
CMOV와 같은 명령어 활용.
- 분기 없이 조건 플래그에 따라 데이터를 이동시키는
- 룩업 테이블
- 조건부 로직을 배열의 사전 계산된 값으로 대체.
- 프레디케이션(predication) 및 선택 명령어
- 프레디케이트에 기반하여 연산을 실행하는 명령어.
- 예: 일부 CPU 아키텍처에서의 3항 연산자.
6. SIMD와 분기 없는 프로그래밍

- SIMD 소개
- 단일 명령어, 다중 데이터: 하나의 명령어로 여러 데이터 포인트를 처리.
- 벡터화
- 스칼라 연산을 벡터 연산으로 변환하는 기술.
- SIMD에서의 분기 없는 기법
- 마스크 및 블렌드(blend) 명령어를 사용하여 분기 없이 조건부 로직 처리.
- 예시
- 대용량 데이터 세트에 병렬로 연산 적용.
- C/C++에서
_mm_blendv_ps와 같은 인트린직 활용.
7. 실용적인 예제
-
예제 1: 절대값 함수
-
전통적인 분기 구현 (C++):
int abs(int x) { if (x < 0) return -x; else return x; } -
비트 조작을 사용한 분기 없는 구현:
int abs(int x) { int mask = x >> (sizeof(int) * 8 - 1); return (x + mask) ^ mask; } -
설명:
x >> 31은 음수이면1(비트가 모두 1), 양수이면0을 반환.- 마스크를 사용하여
x를 조정하여 분기 없이 절대값 계산.
- 예제 2: 값 클램핑(범위 제한)
-
전통적인 분기 구현 (Python):
def clamp(value, min_val, max_val): if value < min_val: return min_val elif value > max_val: return max_val else: return value -
분기 없는 구현:
def clamp(value, min_val, max_val): return max(min_val, min(value, max_val)) -
설명:
min및max함수를 사용하여 조건부 분기 없이 값 제한.
- 예제 3: 루프 최적화
-
분기가 있는 루프 (C++):
for (int i = 0; i < n; ++i) { if (array[i] != 0) { sum += array[i]; } } -
분기 없는 루프 구현:
for (int i = 0; i < n; ++i) { sum += array[i] * (array[i] != 0); } -
또는 SIMD를 사용하여 병렬화:
// SIMD 인트린직을 사용한 예제 (고급 내용) // vectorization 기술 + mask 사용 -
설명:
- 조건부 분기를 제거하고 곱셈을 사용하여 합산.
array[i] != 0은true이면1,false이면0으로 처리.
- 예제 4: 최대값 계산
-
전통적인 분기 구현:
int max(int a, int b) { if (a > b) return a; else return b; }if문을 사용하여 두 값 중 큰 값을 반환합니다. -
분기 없는 구현:
int max(int a, int b) { int diff = a - b; int k = (diff >> 31) & 0x1; return a - k * diff; } -
설명:
diff >> 31은a - b의 부호 비트를 가져옵니다.k는a가b보다 크면0, 작으면1이 됩니다.a - k * diff를 계산하여 큰 값을 반환합니다.
- 예제 5: 최소값 계산
-
전통적인 분기 구현:
int min(int a, int b) { if (a < b) return a; else return b; }if문을 사용하여 두 값 중 작은 값을 반환합니다. -
분기 없는 구현:
int min(int a, int b) { int diff = a - b; int k = (diff >> 31) & 0x1; return b + k * diff; } -
설명:
diff >> 31은a - b의 부호 비트를 가져옵니다.k는a가b보다 작으면1, 크면0이 됩니다.b + k * diff를 계산하여 작은 값을 반환합니다.
- 예제 6: 부호 함수 구현
-
전통적인 분기 구현:
int sign(int x) { if (x > 0) return 1; else if (x < 0) return -1; else return 0; }if문을 사용하여 수의 부호를 반환합니다. -
분기 없는 구현:
int sign(int x) { return (x > 0) - (x < 0); } -
설명:
(x > 0)은true이면1,false이면0입니다.(x < 0)은true이면1,false이면0입니다.- 두 값을 빼서
1,0,1중 하나를 반환합니다.
- 예제 7: 조건부 값 선택
-
전통적인 분기 구현:
int select(bool condition, int true_val, int false_val) { if (condition) return true_val; else return false_val; }if문을 사용하여 조건에 따라 값을 선택합니다. -
분기 없는 구현:
int select(bool condition, int true_val, int false_val) { return false_val ^ ((true_val ^ false_val) & -int(condition)); } -
설명:
int(condition)는condition이true이면1,false이면0이 됩니다.- 비트 연산을 통해 조건부로 값을 선택합니다.
- 예제 8: 값의 범위 래핑 (Wrapping)
-
전통적인 분기 구현:
int wrap(int value, int lower, int upper) { int range = upper - lower + 1; if (value < lower) return upper - ((lower - value - 1) % range); else if (value > upper) return lower + ((value - upper - 1) % range); else return value; }조건문을 사용하여 값을 지정된 범위 내로 래핑합니다.
-
분기 없는 구현:
int wrap(int value, int lower, int upper) { int range = upper - lower + 1; return lower + ((value - lower) % range + range) % range; } -
설명:
- 수학적 연산을 사용하여 분기 없이 값을 래핑합니다.
- 모듈로 연산을 두 번 사용하여 음수 값을 처리합니다.
- 예제 9: 조건부 합산
-
전통적인 분기 구현:
int conditional_add(int sum, int value, bool condition) { if (condition) return sum + value; else return sum; }조건에 따라 값을 합산합니다.
-
분기 없는 구현:
int conditional_add(int sum, int value, bool condition) { return sum + (value * condition); } -
설명:
condition이true이면1,false이면0으로 간주되어 곱셈으로 합산 결정.
- 예제 10: 비트 반전 없이 음수 만들기
-
분기 없는 구현:
int negate(int x) { return ~x + 1; } -
설명:
- 2의 보수를 사용하여 분기 없이 음수를 만듭니다.
- 예제 11: 배열 요소 임계값 처리
-
전통적인 분기 구현:
void threshold(int* data, size_t size, int threshold) { for (size_t i = 0; i < size; ++i) { if (data[i] > threshold) { data[i] = threshold; } } }조건문을 사용하여 각 배열 요소가 임계값을 초과하면 임계값으로 설정합니다.
-
분기 없는 SIMD 구현:
#includevoid threshold_simd(int* data, size_t size, int threshold) { size_t i = 0; __m256i v_threshold = _mm256_set1_epi32(threshold); // 임계값을 모든 요소에 복사
// 8개의 정수를 한 번에 처리 for (; i + 7 < size; i += 8) { // 데이터 로드 __m256i v_data = _mm256_loadu_si256((__m256i*)&data[i]); // 데이터와 임계값의 최소값 계산 __m256i v_result = _mm256_min_epi32(v_data, v_threshold); // 결과 저장 _mm256_storeu_si256((__m256i*)&data[i], v_result); } // 남은 요소 처리 for (; i < size; ++i) { if (data[i] > threshold) { data[i] = threshold; } }}
-
설명:
- SIMD 명령어
_mm256_min_epi32를 사용하여 분기 없이 각 요소를 임계값과 비교하여 작은 값을 선택합니다. - 한 번에 8개의 요소를 처리하여 성능을 향상시킵니다.
- 분기를 제거하여 분기 예측 실패로 인한 오버헤드를 감소시킵니다.
- SIMD 명령어
- 예제 12: 음수 값을 0으로 설정
-
전통적인 분기 구현:
void zero_negative(int* data, size_t size) { for (size_t i = 0; i < size; ++i) { if (data[i] < 0) { data[i] = 0; } } }조건문을 사용하여 배열에서 음수 값을 찾아 0으로 만듭니다.
-
분기 없는 SIMD 구현:
#includevoid zero_negative_simd(int* data, size_t size) { size_t i = 0; __m256i zero = _mm256_setzero_si256(); // 모든 요소가 0인 벡터
// 8개의 정수를 한 번에 처리 for (; i + 7 < size; i += 8) { // 데이터 로드 __m256i v_data = _mm256_loadu_si256((__m256i*)&data[i]); // 음수인 요소를 찾기 위한 마스크 생성 __m256i mask = _mm256_cmpgt_epi32(zero, v_data); // 음수인 요소를 0으로 설정 __m256i v_result = _mm256_blendv_epi8(v_data, zero, mask); // 결과 저장 _mm256_storeu_si256((__m256i*)&data[i], v_result); } // 남은 요소 처리 for (; i < size; ++i) { if (data[i] < 0) { data[i] = 0; } }}
-
설명:
_mm256_cmpgt_epi32를 사용하여 음수인 요소에 대한 마스크를 생성합니다._mm256_blendv_epi8를 통해 마스크에 따라 음수인 요소를 0으로 설정합니다.- 분기 없는 SIMD 연산을 통해 처리 속도를 높입니다.
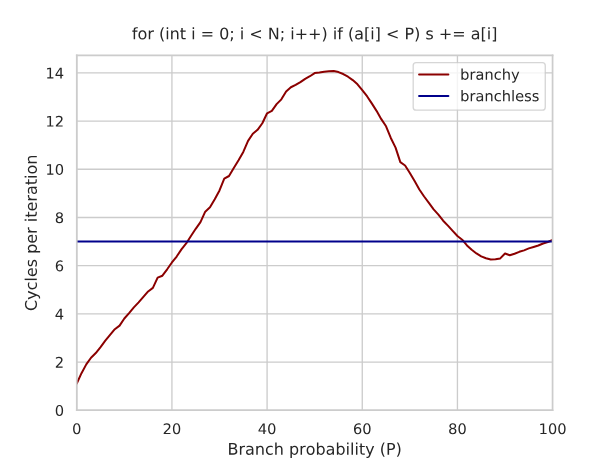
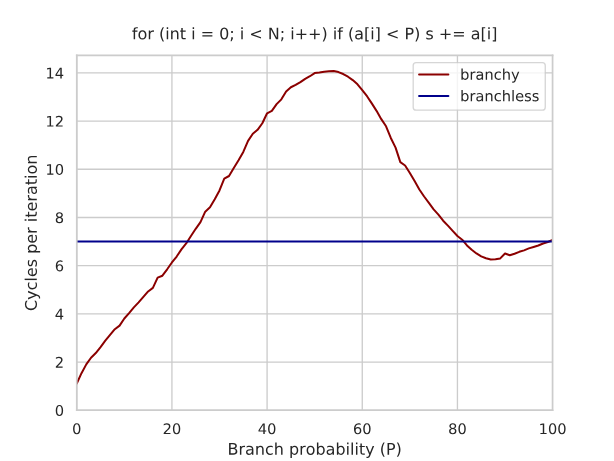
- 벤치마킹 결과
- 분기 있는 코드와 분기 없는 코드의 성능 비교 차트 제공.
- 사이클 카운트, 실행 시간 등의 메트릭.
-
8. 도구 및 기술
- 프로파일링 및 벤치마킹
perf,gprof,Intel VTune등의 도구를 사용하여 병목 지점 식별.
- 컴파일러 최적화
- 현대 컴파일러가 코드를 최적화하는 방법과 생성된 어셈블리를 이해하는 중요성.
- 인트린직 및 저수준 프로그래밍
- 최적화를 위한 CPU 특정 명령어 활용.
- 정적 분석
- 코드 경로를 분석하고 잠재적인 분기를 식별하는 도구.
9. 잠재적인 단점
- 코드 가독성 및 유지보수성
- 분기 없는 코드는 직관적이지 않고 이해하기 어려울 수 있음.
- 일부 경우의 오버헤드
- 모든 코드가 분기 없는 기법의 이점을 얻는 것은 아니며, 때로는 분기가 더 빠를 수 있음.
- 하드웨어 고려 사항
- CPU 아키텍처의 차이가 성능 향상에 영향을 줄 수 있음.
- 디버깅 복잡성
- 복잡한 코드 경로는 디버깅을 더 어렵게 만들 수 있음.
10. 모범 사례
-
균형 잡힌 접근
-
성능과 코드 명확성 간의 트레이드오프 평가.
-
-
점진적인 최적화
- 프로파일링을 통해 식별된 중요한 코드 경로에 초점.
- 테스트 및 검증
- 최적화가 프로그램의 정확성을 변경하지 않도록 보장.
- 하드웨어 트렌드 업데이트
- 새로운 CPU 기능 및 명령어 세트에 대한 최신 정보 유지.
 Isaac's Tech Blog
Isaac's Tech Blog